Triangles rectangles presque isocèles

Dans cette note, nous traitons chacune des questions du quatrième exercice du sujet de mathématiques du Baccalauréat S, Enseignement de Spécialité, session de juin 2017 en France métropolitaine. Cet exercice a pour thème les triangles rectangles presque isocèles.

Un triangle rectangle presque isocèle, en abrégé TRPI, est un triangle rectangle dont les côtés de l’angle droit ont pour longueurs respectives $x$ et $x+1$ , et dont l’hypoténuse a pour longueur $y$ , où $x$ et $y$ sont des entiers naturels.

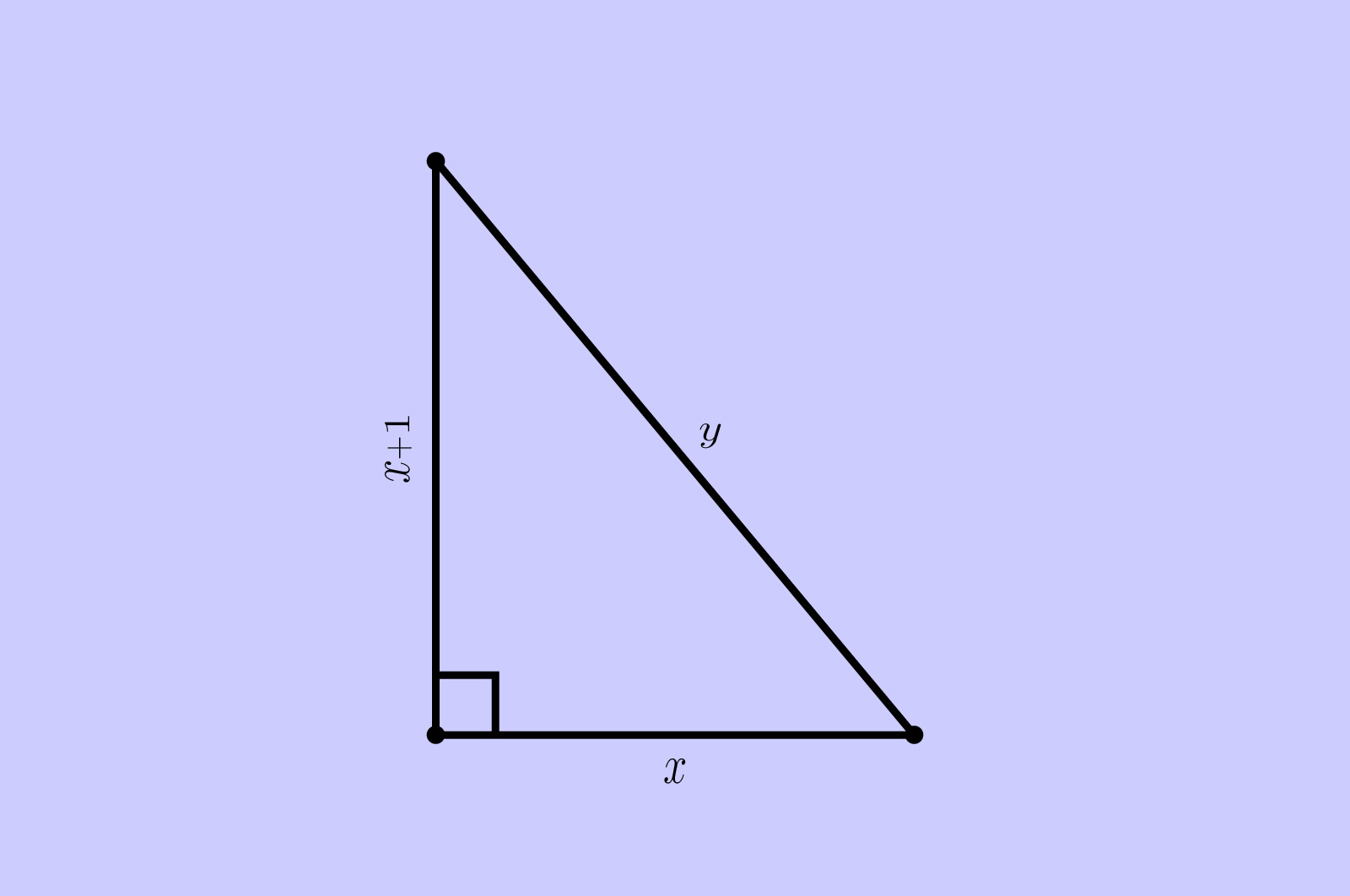
Autrement dit, un TRPI est un triangle rectangle dont les longueurs des côtés de l’angle droit sont deux nombres entiers consécutifs et dont la longueur de l’hypoténuse est un nombre entier.

Si un triangle de côtés $x$ , $x+1$ et $y$ , où $y$ est la longueur de l’hypoténuse, est un TRPI, on dit que le couple $(x,y)$ définit un TRPI.

Partie A.

(1) Un couple $(x,y)$ d’entiers naturels définit un TRPI si et seulement si $y^{2}=2x^{2}+2x+1$ .

D’après le théorème de Pythagore, un couple $(x,y)$ d’entiers naturels définit un TRPI si et seulement si $y^{2}=x^{2}+(x+1)^2$ . Ceci équivaut à

$\displaystyle y^{2}=2x^{2}+2x+1$ ,

puisque $(x+1)^{2}=x^{2}+2x+1$ .

(2) Le TRPI ayant les plus petits côtés non nuls est défini par le couple $(3,5)$ .

Soit la fonction $f:\mathbb{R}\rightarrow\mathbb{R}$ définie par $f(x)=2x^{2}+2x+1$ . Alors, à l’évidence, un couple $(x,y)$ d’entiers naturels définit un TRPI si et seulement si $f(x)$ est un carré parfait avec $f(x)=y^{2}$ . Cependant, $f(1)=5$ et $f(2)=13$ ne sont des carrés parfaits. À l’inverse,

$\displaystyle f(3)=2\times 3^{2}+2\times 3+1=25=5^{2}$ .

Par conséquent, le TRPI ayant les plus petits côtés non nuls est défini par le couple $(3,5)$ .

(3.a) Si le carré d’un entier naturel est impair, alors il en est de même pour celui-ci.

Soit $n$ un nombre entier naturel pair. Alors, il existe un nombre $k\in\mathbb{N}$ tel que $n=2k$ . Donc, $n^{2}=4k^{2}$ est pair. Ainsi, la parité de $n$ implique celle de $n^{2}$ . Eu égard à la règle de contraposition, il en résulte que, si $n^{2}$ est impair, alors $n$ est impair.

(3.b) Dans un couple $(x,y)$ d’entiers naturels définissant un TRPI, le nombre $y$ est nécessairement impair.

Soit $(x,y)$ un couple d’entiers naturels définissant un TRPI. Alors, $y^{2}=2k+1$ avec $k=x^{2}+x$ , selon (A.1). Le nombre $y^{2}$ est donc impair. D’après (A.3.a), il en est de même pour $y$ .

(4) Si un couple $(x,y)$ d’entiers naturels définit un TRPI, alors $x$ et $y$ sont premiers entre eux.

Soit $(x,y)$ un couple d’entiers naturels définissant un TRPI. Alors,

$\displaystyle y^{2}=2x^{2}+2x+1$ ,

c’est-à-dire $ax+by=1$ , où $a=-(2x+2)$ et $b=y$ . En vertu du théorème de Bezout, il s’ensuit que les nombres $x$ et $y$ sont premiers entre eux.

Partie B.

Soit la matrice carrée $A=\left(\begin{array}{l@{\quad}r}3 & 2 \\[3pt] 4 & 3\end{array}\right)$ et la matrice colonne $B=\left(\begin{array}{c}1 \\[3pt] 2\end{array}\right)$ . Soient par ailleurs $x$ et $y$ des nombres entiers naturels. Les entiers naturels $x^{\prime}$ et $y^{\prime}$ sont du reste définis par la relation

$\displaystyle \left(\begin{array}{c}x^{\prime} \\[3pt] y^{\prime}\end{array}\right)=A\left(\begin{array}{c}x \\[3pt] y\end{array}\right)+B$ .

(1) Expression de $x^{\prime}$ et $y^{\prime}$ en fonction $x$ et $y$ .

Par définition,

$\displaystyle \left(\begin{array}{c}x^{\prime} \\[3pt] y^{\prime}\end{array}\right)=\left(\begin{array}{l@{\quad}r}3 & 2 \\[3pt] 4 & 3\end{array}\right)\left(\begin{array}{c}x \\[3pt] y\end{array}\right)+\left(\begin{array}{c}1 \\[3pt] 2\end{array}\right)$ .

De ce fait,

$\displaystyle \left\{\begin{array}{l}x^{\prime}=3x+2y+1, \\[6pt] y^{\prime}=4x+3y+2.\end{array}\right.$

(2.a) Montrons que $(y^{\prime})^{2}-2x^{\prime}(x^{\prime}+1)=y^{2}-2x(x+1)$ .

Des calculs simples livrent

$\displaystyle (y^{\prime})^{2}=16x^{2}+9y^{2}+24xy+16x+12y+4$

$2x^{\prime}(x^{\prime}+1)=18x^{2}+8y^{2}+24xy+18x+12y+4$ .

Par conséquent,

$\displaystyle (y^{\prime})^{2}-2x^{\prime}(x^{\prime}+1)=-2x^{2}+y^{2}-2x=y^{2}-2x(x+1)$ .

(2.b) Si le couple $(x,y)$ définit un TRPI, alors le couple $(x^{\prime},y^{\prime})$ définit également un TRPI.

Soit $(x,y)$ un couple d’entiers naturels définissant un TRPI. Alors, $y^{2}-2x(x+1)=1$ . Ceci induit $(y^{\prime})^{2}-2x^{\prime}(x^{\prime}+1)=1$ . Par conséquent, le couple $(x^{\prime},y^{\prime})$ définit également un TRPI.

Soient $(x_{n})_{n\in\mathbb{N}}$ et $(y_{n})_{n\in\mathbb{N}}$ les suites d’entiers naturels définies par $x_{0}=3$ et $y_{0}=5$ , puis

$\displaystyle \left(\begin{array}{c}x_{n+1} \\[3pt] y_{n+1}\end{array}\right)=A\left(\begin{array}{c}x_{n} \\[3pt] y_{n}\end{array}\right)+B$

pour tout entier naturel $n$ .

(3) Pour tout entier naturel $n$ , le couple $(x_{n}, y_{n})$ définit un TRPI.

Ce fait est notoirement vrai pour $n=0$ (voir notamment (A.2)). Au demeurant, si, pour un entier naturel $n$ quelconque, le couple $(x_{n},y_{n})$ définit un TRPI, alors le couple $(x_{n+1},y_{n+1})$ aussi définit un TRPI, d’après (B.2.b). Eu égard à la règle de récurrence, il en découle que le couple $(x_{n}, y_{n})$ définit un TRPI pour chaque $n\in\mathbb{N}$ .

(4) Détermination d’un TRPI dont les longueurs des côtés sont supérieures à $2017$ .

Il suffit de calculer les premiers termes des suites $x_{n}$ et $y_{n}$ . Ces calculs conduisent au tableau suivant.

$\begin{array}{|c|c|c|c|c|c|} \hline n & 0 & 1 & 2 & 3 & 4 \\[0pt] \hline x_{n} & 3 & 20 & 119 & 696 & 4059 \\[0pt] \hline y_{n} & 5 & 29 & 169 & 985 & 5741 \\[0pt] \hline \end{array}$

Le couple $(4059,5741)$ définit donc un TRPI dont les longueurs des côtés sont supérieures à $2017$ .

Réaliser un don pour nous encourager à produire plus de contenus.

Choisir un montant

€5,00

€15,00

€100,00

Ou saisissez un montant personnalisé :

€

Votre contribution est appréciée.

Faire un don

Publicités

Formalis Mathematica

Rigueur et formalisme au cœur de l’apprentissage et de l’enseignement des mathématiques

Triangles rectangles presque isocèles

Réaliser un don pour nous encourager à produire plus de contenus.

Laisser un commentaire Annuler la réponse.

Réaliser un don pour nous encourager à produire plus de contenus.

Partagez :

Similaire

Laisser un commentaire Annuler la réponse.