Lors d’un math de rugby, un joueur doit transformer un essai qui a été marqué au point situé à l’extérieur du segment
. La transformation consiste à taper le ballon par un coup de pied depuis un point
que le joueur a le droit de choisir n’importe où sur le segment
perpendiculaire à la droite
sauf en
. La transformation est réussie si le ballon passe entre les poteaux repérés par les points
et
sur la figure ci-dessous.
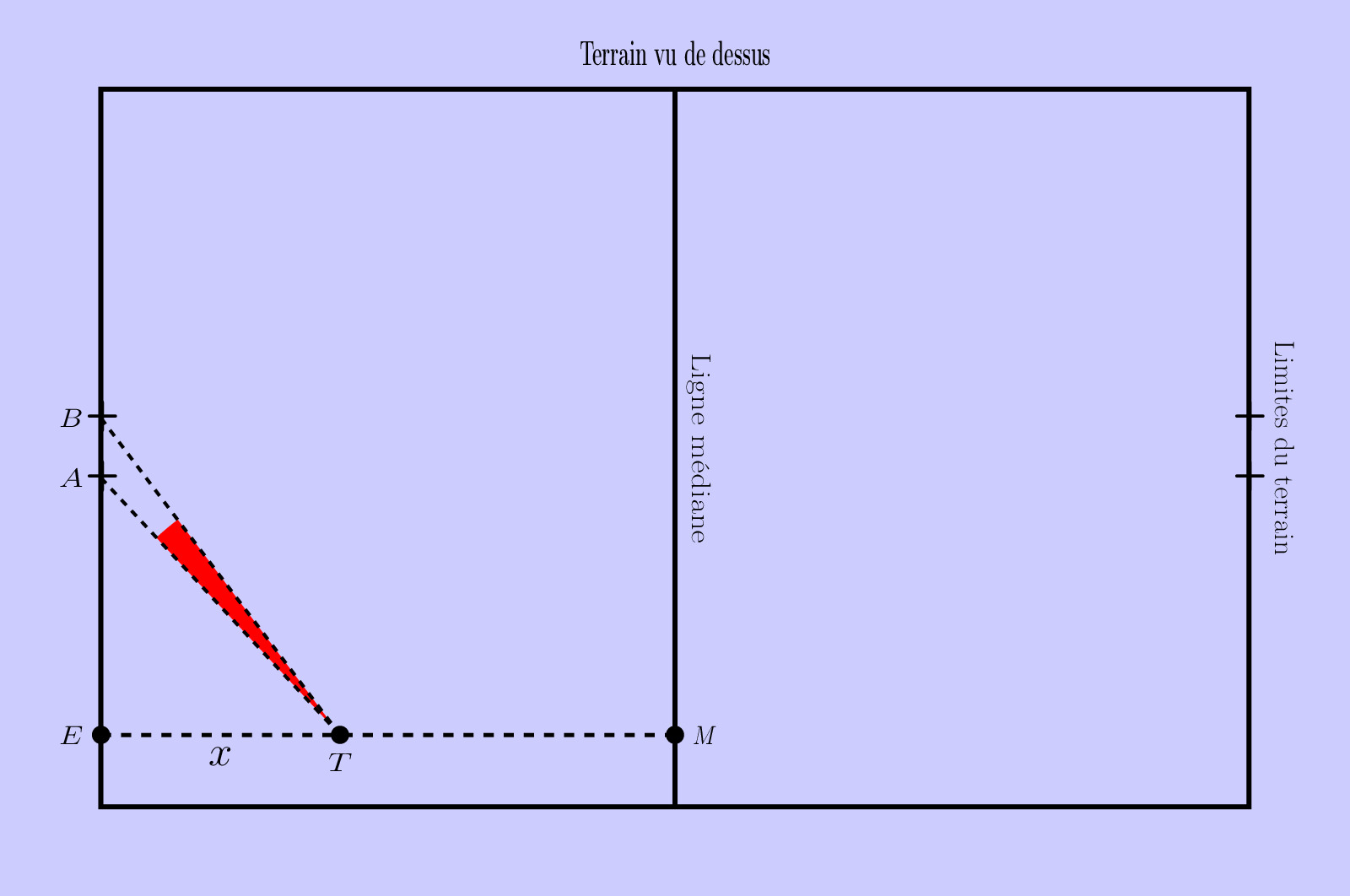
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point qui rend l’angle
le plus grand possible.
Le but de cet exercice est donc de rechercher s’il existe une position du point sur le segment
pour laquelle l’angle
est maximum et, si c’est le cas, de déterminer une valeur approchée de cet angle. Dans toute la suite, on note la longueur
, qu’on cherche à déterminer.
Les dimensions du terrain sont les suivantes :
.
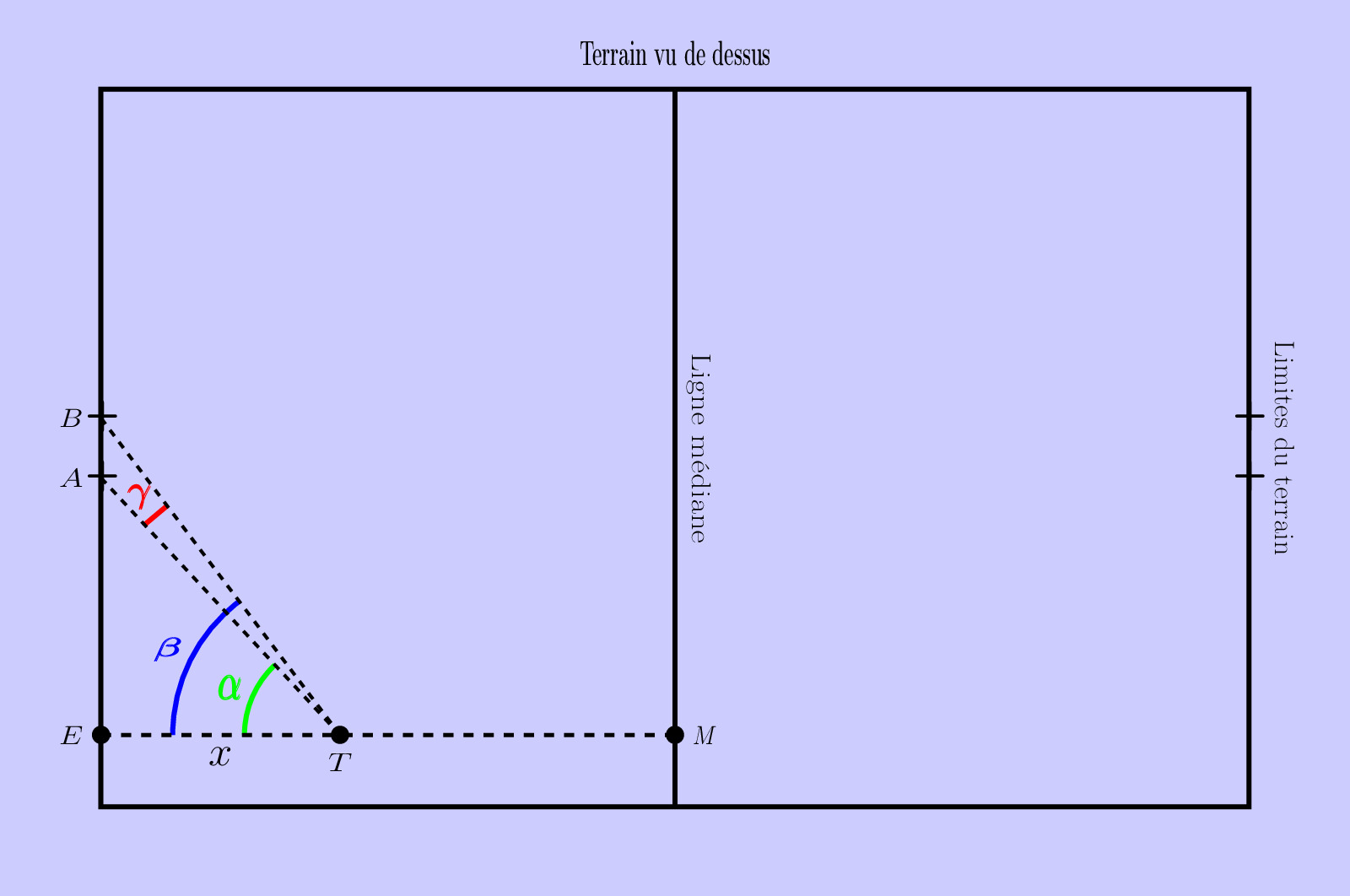
Soit la mesure en radian de l’angle
, puis
la mesure en radian de l’angle
et
la mesure en radian de l’angle
.
1) Expression de
et
en fonction de
.
En utilisant les triangles rectangles et
ainsi que les longueurs fournies, nous exprimons
et
en fonction de
. En effet,
et
.
2) La fonction
est strictement croissante sur l’intervalle
.
En effet, définie sur notamment l’intervalle par
, elle est dérivable en tant que quotient de fonctions dérivables. Du reste,
pour chaque . La fonction tangente est donc strictement croissante sur l’intervalle
, car sa dérivée est strictement positive sur ledit intervalle.
3) La tangente de
s’exprime par
.
Chacun des angles et
, angle d’un triangle rectangle est aigu. De ce fait, leurs mesures respecctives
et
appartiennent à l’intervalle
. En outre, le point
, distinct de
et de
, appartient au segment
. De ce fait,
.
Autrement dit,
.
Par conséquent, .
Maintenant, considérons des réels et
contenus dans l’intervalle
. Alors,
.
Par conséquent,
.
Donc,
pour tous réels et
de l’intervalle
. Il en résulte que
,
c’est-à-dire
.
4) L’angle
est maximum lorsque sa mesure
est maximale. Cela correspond à un minimum sur l’intervalle
de la fonction
définie par
.
La fonction tangente étant strictement croissante sur l’intervalle , l’angle
est maximum lorsque
est maximum. Or,
où et
. Il s’ensuit que l’angle
est maximum lorsque le réel
est minimal pour
.
Il suffit donc d’étudier la fonction dans l’intervalle
pour déduire la valeur maximale de
, la mesure de l’angle
.
La fonction est dérivable sur l’intervalle
en tant que somme d’une fonction polynôme et d’un scalaire de la fonction inverse. Du reste,
pour chaque . De ce fait, la dérivée de
est nulle pour
, strictement négative sur
, et strictement positive sur
. Par ailleurs,
.
Ces informations permettent de dresser le tableau de variation suivant.
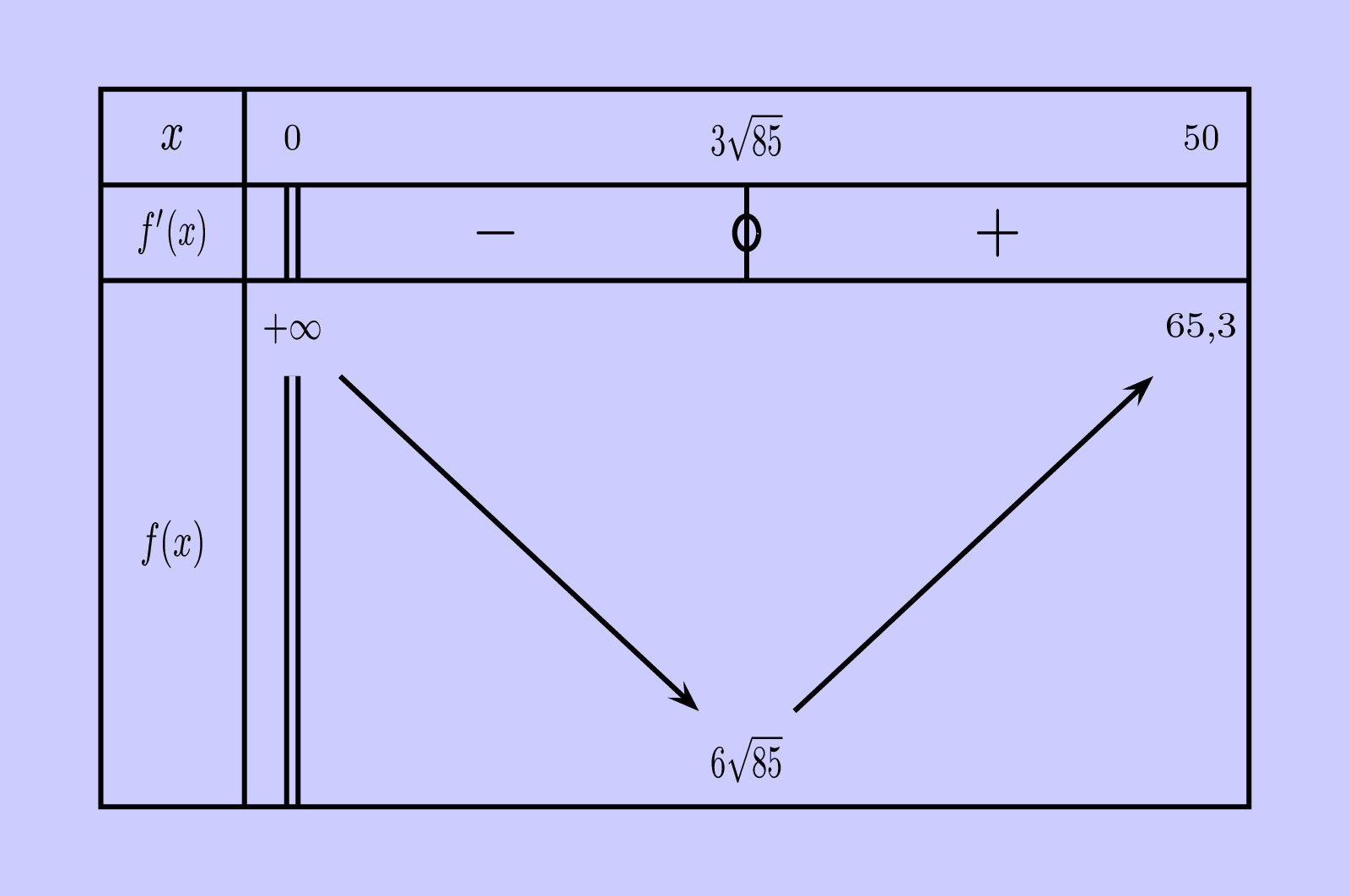
Celui-ci révèle que, dans l’intervalle , la fonction
est minimale pour
. Ce minimum correspond à la valeur maximale de
. Autrement dit, la tangente de la mesure maximale de l’angle
est
.
Par conséquent, la mesure maximale de l’angle est
.
Elle correspond à la valeur
.
Cette contribution est largement inspirée de l’Exercice 4 de l’épreuve de mathématiques du baccalauréat général 2016, série S, enseignement obligatoire, en France métropolitaine. Elle mobilise des éléments de la théorie des angles et de leur mesure, de la trigonométrie et de la théorie des fonctions numériques d’une variable réelle.
Les angles et leur mesure sont étudiés avec soin dans le Volume I du Discours formel sur les mathématiques pour le secondaire. Le Volume II à paraître est quant à lui dédié aux fonctions numériques d’une variable réelle. Il y est du reste aussi question de trigonométrie et de fonctions trigonométriques.
Réaliser un don pour nous encourager à produire plus de contenus.
Choisir un montant
Ou saisissez un montant personnalisé :
Votre contribution est appréciée.
Faire un don