Dans les langages formels de la logique classique, des expressions peuvent être construites au moyen de la négation () ou de connecteurs tels que la disjonction (), la conjonction (), l’implication () et l’équivalence (). La sémantique de telles expressions est définie par les tables de vérités ci-dessous.

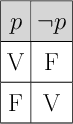
Dans ce billet, nous présentons un autre connecteur logique : la disjonction exclusive.

Dans un langage formel, si et désignent des expressions, alors une expression composée est définie par

.

Elle est appelée disjonction exclusive de et , ou encore alternative entre et . De plus, un contexte étant associé à ce langage formel, la disjonction exclusive  est vraie lorsque une et une seule des assertions et est vraie. En d’autres termes, la table de vérité de la disjonction exclusive est donnée comme suit.

Le connecteur est appelé « ou exclusif » et chaque disjonction exclusive se traduit littéralement par « soit , soit « . À l’évidence, pour toute assertion , la composée est vraie. Du reste, l’opérateur est commutatif. En d’autres termes, pour des assertions et quelconques, l’équivalence est vraie.

La disjonction exclusive correspond à la négation de l’équivalence. Autrement dit, l’équivalence est vraie pour toutes les assertions et . Par ailleurs, l’assertion est logiquement équivalente à chacune des composées suivantes:

,

puis

.

Ces équivalences logiques s’établissent facilement au moyen de tables de vérité. À cet égard, le Volume I du Discours formel sur les mathématiques pour le secondaire présente des informations détaillées, dans le fil d’un traitement systématique de la logique mathématique.