Dans cette brève, nous nous proposons de résoudre dans l’équation diophantienne suivante:
À cet effet, nous considérons le résultat suivant :
Proposition 1. Pour tout couple
d’entiers relatifs, la relation
est équivalente à
.
Preuve. Soit un couple . Alors,
, car
.
Ainsi, si et seulement si
. Ceci signifie que
.
La solution de l’équation est donnée par la proposition suivante :
Proposition 2. Un triplet
d’entiers relatifs est solution de l’équation diophantienne
si et seulement s’il existe un triplet
vérifiant
.
Preuve. Soit un triplet d’entiers relatifs tel que
. Alors,
. Donc,
. De ce fait,
, selon la Proposition 1. Maintenant, soit
le reste de la division euclidienne de
par
. Alors,
. Du reste, en raison de la congruence
, cet entier
est également le reste de la division euclidienne de
par
. Ainsi, il existe un couple
tel que
et
. Par conséquent,
, c’est-à-dire
.
Donc,
,
où et
sont des entiers relatifs et
. Cependant, pour chaque triplet
, nous avons
.
Ceci conclut la preuve de la proposition 2.
Pour plus d’exercices d’arithmétique, consultez l’ouvrage suivant :
Réaliser un don pour nous encourager à produire plus de contenus.
Choisir un montant
Ou saisissez un montant personnalisé :
Votre contribution est appréciée.
Faire un don
Bonjour.
Comment traiter vous ce cas 3x+13y+23z =59?
J’aimeJ’aime
Bonne question !
Dans quelques jours, je publierai un article sur une situation plus générale qui répondra à votre question.
J’aimeJ’aime
Avant un traitement plus général, voici ma réponse à votre question.
L’équation est soluble dans
est soluble dans  pour tout entier relatif
pour tout entier relatif 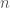 .
.
En effet, . De ce fait,
. De ce fait,  équivaut à
équivaut à  . Il en résulte que l’ensemble des solutions de l’équation initiale est constitué des triplets
. Il en résulte que l’ensemble des solutions de l’équation initiale est constitué des triplets  , où
, où 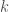 et
et  sont des entiers relatifs, puis
sont des entiers relatifs, puis  .
.
J’aimeJ’aime
Parfait…
J’aimeJ’aime
https://formalismathematica.wordpress.com/2019/10/16/methode-generale-de-resolution-des-equations-diophantiennes-a-trois-inconnues/
J’aimeJ’aime
Merci
J’aimeJ’aime